Find Out the Heat of Solution of Kno3

Heat of Solution or Enthalpy of Solution Chemistry Tutorial
Key Concepts
- A solute dissolves in excess solvent to form a solution:
solute + solvent → solution
- Heat of solution, or, enthalpy of solution, is the energy released or absorbed when the solute dissolves in the solvent.
- Molar heat of solution, or, molar enthalpy of solution, is the energy released or absorbed per mole of solute being dissolved in solvent.
- Heat of solution (enthalpy of solution) has the symbol1 ΔHsoln
- Molar heat of solution (molar enthalpy of solution) has the units2 J mol-1 or kJ mol-1
- If heat is released when the solute dissolves, temperature of solution increases, reaction is exothermic, and ΔH is negative.
solute + solvent → solution ΔHsoln = -
If heat is absorbed when the solute dissolves, temperature of solution decreases, reaction is endothermic, and ΔH is positive.
solute + solvent → solution ΔHsoln = +
- Enthalpy (heat) of solution can be determined in the laboratory by measuring the temperature change of the solvent when solute is added.
- To calculate the enthalpy of solution (heat of solution) using experimental data:
Step 1: Amount of energy released or absorbed is calculated
q = m × Cg × ΔT q = amount of energy released or absorbed
m = mass
Cg = specific heat capacity
ΔT = change in temperature
Step 2: calculate moles of solute
n = m ÷ M n = moles of solute
m = mass of solute
M = molar mass of solute
Step 3: Amount of energy (heat) released or absorbed per mole of solute is calculated
ΔHsoln = q ÷ n ΔHsoln = molar enthalpy (heat) of solution
q = amount of energy (heat) released or absorbed
n = moles of solute
ΔH is negative if energy (heat) is released (exothermic).
ΔH is positive if energy (heat) is absorbed (endothermic).
Please do not block ads on this website.
No ads = no money for us = no free stuff for you!
Theory Behind Determining Molar Enthalpy of Solution
The molecules or ions making up a solid solute exist in a highly ordered state which is referred to as a lattice.
You are probably already familiar with representations of ionic compounds in which positive ions (cations) and negative ions (anions) are arranged in a lattice held together by electrostatic forces of attraction known as ionic bonds.
The amount of disorder, or randomness, in a system is known as its entropy. A lattice is highly ordered, that is, the particles making up the lattice are in a low state of disorder. This is referred to as a low entropy state3.
When this solute dissolves in a solvent, particles such as ions must be removed from the lattice and each solute particle must then be completely surrounded by solvent molecules.
The solute particles in the solution are in constant motion and distributed more or less randomly throughout the solution so that the amount of disorder has increased compared to when they were part of the lattice. Solute particles in the solution are said to be in a higher state of entropy than solute particles making up the lattice.
The process of dissolving a solid solute in a liquid solvent can therefore be thought of as occurring in two steps:
If Enthalpy (heat) of Solution is Endothermic: The magnitude of the energy absorbed to break up the lattice, ΔHlat, is greater than the magnitude of the energy released when solute particles are surrounded by water solvent molecules, ΔHhyd, so the enthalpy of solution, ΔHsoln, is positive, that is, the process is endothermic. if |ΔHlat| > |ΔHhyd| then ΔHsoln is positive solute (s) + water (l) → solution(aq) ΔHsoln = + solute (s) + water (l) + ΔH → solution(aq) Energy is absorbed, that is, energy is a reactant. When solute is added to water, water temperature decreases. |
|
If Enthalpy (heat) of Solution is Exothermic: The magnitude of the energy absorbed to break up the lattice is less than magnitude of the energy released when solute particles are surrounded by water solvent molecules , so the enthalpy of solution is negative, that is, the process is exothermic. if |ΔHlat| < |ΔHhyd| then ΔHsoln is negative solute (s) + water (l) → solution(aq) ΔHsoln = - solute (s) + water (l) → solution(aq) + ΔH Energy is released, that is, energy is a product. When solute is added to water, water temperature increases. |
|
The table below lists the values of molar enthalpy (heat) of solution for some common salts in water at 25°C.4
| Molar Enthalpy of Solution of Some Salts at 25°C | |||||
|---|---|---|---|---|---|
| Endothermic examples | Exothermic examples | ||||
| Anion | solute | ΔHo soln / kJ mol-1 | solute | ΔHo soln / kJ mol-1 | |
| chloride | NH4Cl(s) | +14.78 | LiCl(s) | -37.03 | |
| NaCl(s) | +3.88 | ||||
| KCl(s) | +17.22 | ||||
| bromide | NH4Br(s) | +16.78 | LiBr(s) | -23.26 | |
| KBr(s) | +19.87 | NaBr(s) | -0.60 | ||
| nitrate | NH4NO3(s) | +25.69 | LiNO3(s) | -2.51 | |
| AgNO3(s) | +22.59 | ||||
| NaNO3(s) | +20.50 | ||||
| KNO3(s) | +34.89 | ||||
| hydroxide | LiOH(s) | -23.56 | |||
| NaOH(s) | -44.51 | ||||
| KOH(s) | -57.61 | ||||
| acetate | NH4C2H3O2(s) | -2.38 | |||
| NaC2H3O2(s) | -17.32 | ||||
| KC2H3O2(s) | -15.33 | ||||
Experiment to Determine the Molar Heat of Solution (Molar Enthalpy of Solution) of a Solute
The following describes the use of a polystyrene foam (styrofoam™) cup as a calorimeter to determine the heat of solution of a salt (solid solute) in water (the solvent).5
Polystyrene foam (styrofoam™) is a good insulator, that is, it is a material that does not conduct heat well.
In this experiment the polystyrene foam (styrofoam™) cup is used as an insulated vessel in which to conduct the experiment so that either:
(i) all the energy released by the reaction is used to raise the temperature of the water in the cup and is not lost in heating the surrounding environment in the case of an exothermic reaction
(ii) the only energy being absorbed by the reaction is that from the water in the cup and not from the surrounding environment in the case of an endothermic reaction.
Procedure:
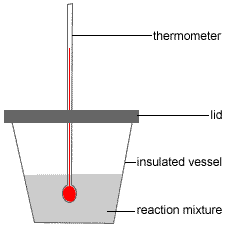
- An accurately known quantity of water (the solvent) is placed in a well insulated vessel (eg, a polystyrene foam or styrofoam™ cup)
- The initial temperature of this reactant is recorded, Ti.
- An accurately known quantity of the solid solute is added, the vessel is sealed with a lid and the solution stirred using the thermometer.
- The final temperature of the reaction mixture is recorded, Tf.
Note the final temperature will be the maximum temperature reached for an exothermic reaction or the minimum temperature reached for an endothermic reaction.
Calculation of Molar Enthalpy (heat) of Solution6
Step 1: Calculate the heat released or absorbed, in joules, when the solute dissolves in the solvent:
heat released or absorbed = mass × specific heat capacity × change in temperature
q = m × cg × (Tfinal - Tinitial )
q = m × cg × ΔT
| What is the value of mass, m? There are 2 ways to look at this: | ||
| 1. Method usually used by High School courses. Assume all the solute dissolves simultaneously in the solvent so that all the heat is simultaneously absorbed from, or released to, the pure solvent. m = mass of solvent in grams So, cg = specific heat capacity of the solvent in J°C-1g-1 ΔT = Tfinal - Tinitial in °C7 When calculated, q is in joules (J) | OR | 2. Method usually used in introductory University courses. Assume the first molecule or ion of solute dissolves into pure solvent, but each subsequent molecule or ion is dissolving into a mixture of dissolved solute in solvent (that is, a solution). In this case, the final solute molecule or ion is dissolving into a solution with a mass approximated by the mass of the solvent plus the mass of the solute. m = mass of solvent + mass of solute in grams So, cg = specific heat capacity of the solution in J°C-1g-1 ΔT = Tfinal - Tinitial in °C7 When calculated, q is in joules (J) |
Step 2: Calculate moles of solute:
moles = mass ÷ molar mass
where:
moles = amount of solute in mole
mass = mass of solute in grams
molar mass = molar mass of solute in grams per mole
Step 3: Calculate the molar enthalpy of solution, or molar heat of solution, ΔHsoln:
| ΔHsoln in J per mole of a solute is calculated: | ΔHsoln in kJ per mole of a solute is calculated: |
|---|---|
| ΔHsoln = q ÷ moles of solute (J mol-1) where exothermic reactions: ΔHsoln is negative endothermic reactions: ΔHsoln is positive | ΔHsoln = q/1000 ÷ moles of solute (kJ mol-1) where exothermic reactions: ΔHsoln is negative endothermic reactions: ΔHsoln is positive |
Sample Experimental Results and Calculations
In a typical experiment, 100 mL of water is placed in the polystyrene foam cup and the initial temperature of the water recorded.
5.05 g potassium nitrate, KNO3(s), is added to the water while stirring.
The temperature of the solution falls and the minimum temperature acheived is recorded as the final temperature.
The results of the experiment are shown in the table below.
| Sample results | ||||
|---|---|---|---|---|
| V(H2O) | = | volume of water | = | 100 mL |
| | ||||
| m(KNO3) | = | mass of KNO3(s) | = | 5.05 g |
| | ||||
| Tinitial | = | initial temperature | = | 25.0°C |
| | ||||
| Tfinal | = | final temperature | = | 21.7°C |
Determine the value of the molar heat of solution of potassium nitrate in kJ mol-1.
(density of water is 1.00 g mL-1 and specific heat capacity of water is 4.18 J°C-1g-1)
| Method 1. (High School Calculations) | Method 2. (Introductory University Calculations) |
|---|---|
| Step 1. Calculate amount of heat released or absorbed. Data from experiment: V = volume of water = 100 mL density of water = 1.00 g mL-1 density = mass ÷ volume cg = specific heat capacity of water = 4.18 J°C-1g-1 ΔT = change in temperature = |Tfinal - Tinitial| | Step 1. Calculate amount of heat released or absorbed. Data from experiment: V = volume of water = 100 mL density of water = 1.00 g mL-1 density = mass ÷ volume msolute = mass of solute = 5.05 g m = mwater + msolute = 100 + 5.05 = 105.05 g cg = specific heat capacity of solution ≈ specific heat capacity of water ΔT = change in temperature = |Tfinal - Tinitial| |
| Calculate q (energy absorbed) q = m × cg × ΔT q = 100 × 4.18 × 3.3 = 1379 J Note: temperature falls, so heat is absorbed. | Calculate q (energy absorbed) q = m × cg × ΔT q = 105.05 × 4.18 × 3.30 = 1449 J Note: temperature falls, so heat is absorbed. |
| Step 2: Calculate moles of solute, n(KNO3) moles solute = mass solute (g) ÷ molar mass solute (g mol-1) n(KNO3) = m(KNO3) ÷ M(KNO3) m(KNO3) = 5.05 g (experimental data) n(KNO3) = 5.05 ÷ 101.11 = 0.0500 mol | Step 2: Calculate moles of solute, n(KNO3) moles solute = mass solute (g) ÷ molar mass solute (g mol-1) n(KNO3) = m(KNO3) ÷ M(KNO3) m(KNO3) = 5.05 g (experimental data) n(KNO3) = 5.05 ÷ 101.11 = 0.0500 mol |
| Step 3: Calculate molar enthalpy of solution, ΔHsoln molar enthalpy of solution = heat absorbed ÷ moles of solute ΔHsoln = q ÷ n(KNO3) q = 1379 J = 1379 ÷ 1000 = 1.379 kJ (from step 1) ΔHsoln = 1.379 kJ ÷ 0.0500 = +27.6 kJ mol-1 ΔHsoln must be positive (+) because energy has been absorbed, that is, the process is endothermic. | Step 3: Calculate molar enthalpy of solution, ΔHsoln molar enthalpy of solution = heat absorbed ÷ moles of solute ΔHsoln = q ÷ n(KNO3) q = 1449 J = 1449 ÷ 1000 = 1.449 kJ (from step 1) ΔHsoln = 1.449 kJ ÷ 0.0500 = +29.0 kJ mol-1 ΔHsoln must be positive (+) because energy has been absorbed, that is, the process is endothermic. |
| Note that the experimental value for ΔHsoln is less than the value in the table (ΔHsoln = +34.89 kJ mol-1). If the system is not well insulated, energy from the surroundings will be absorbed as well as energy from the water so that the fall of water temperature will not be as great as expected. | |
Worked Example of Calculating Molar Enthalpy of Solution
Question:
A student added 4.00 g of NaOH(s) to 100 g of water in a polystyrene foam cup.
The temperature of the water rose by 10.0°C.
Assuming the polystyrene foam cup is well insulated and the specific heat capacity of water is 4.18 J°C-1g-1, determine the molar enthalpy of solution of sodium hydroxide in kJ mol-1.
Solution:
(based on the StoPGoPS method for problem solving)
| STOP | STOP! State the Question. | |||||||||||||||||||||||||||||||||
| What is the question asking you to do? Calculate the molar heat of solution of sodium hydroxide in kJ mol-1 ΔHsoln = ? kJ mol-1 | ||||||||||||||||||||||||||||||||||
| PAUSE | PAUSE to Prepare a Game Plan | |||||||||||||||||||||||||||||||||
| (1) What information (data) have you been given in the question? m(NaOH) = mass NaOH(s) = 4.00 g m(H2O) = mass H2O(l) = 100 g ΔT = temperature increase = 10.0°C cg(H2O) = specific heat capacity of water = 4.18 J°C-1g-1 (2) What is the relationship between what you know and what you need to find out?
Note: ΔHsoln will be negative because the temperature increased, that is, the process is exothermic. | ||||||||||||||||||||||||||||||||||
| GO | GO with the Game Plan | |||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||
| PAUSE | PAUSE to Ponder Plausibility | |||||||||||||||||||||||||||||||||
| Is your answer plausible? Work backwards:
Since this value for the change in temperature is the same as that given in the question, we are confident our answer is correct. | ||||||||||||||||||||||||||||||||||
| STOP | STOP! State the Solution | |||||||||||||||||||||||||||||||||
| State your solution to the problem. Method 1: Molar enthalpy of solution of sodium hydroxide is -41.8 kJ mol-1 Method 2: Molar enthalpy of solution of sodium hydroxide is -43.5 kJ mol-1 | ||||||||||||||||||||||||||||||||||
A student added 1.92 g of KBr(s) to 100 g of water in an insulated vessel. The temperature of the water fell by 0.766°C. Calculate ΔHsoln in kJ mol-1.
Footnotes
1. If the solute and the solvent are in their standard states, you can also write ΔHo sol
Refer to Standard Enthalpy (heat) of Formation and Reaction
2. You may also units of cal mol-1 or kcal mol-1
1 calorie = 4.18 joules
1 cal = 4.18 J
For conversions between J, kJ, and cal refer to energy conversions
3. Entropy refers to the amount of disorder, or randomness, in a system.
Ions locked into a crystal structure are in a low state of disorder and therefore have low entropy.
Ions moving randomly through the solvent molecules in a solution are much more disordered, much more random, so they are said to be in a higher state of entropy.
Gas molecules moving randomly in the atmosphere are in an even greater state of disorder or randomness, so they are said to have an even higher state of entropy.
Moving towards a higher state of entropy is one of the driving forces for a chemical reaction.
4. The values given are for solutions at infinite dilution which is the enthalpy change when 1 mole of solute in its standard state is dissolved in an infinite amount of water.
5. Go to Calorimetry Tutorial to see an alternative method used an adiabatic solution calorimeter.
6. On this page the calculations assume that there is a large excess of solvent
Note that the following examples all use the specific heat capacity of the solvent, cg, not molar heat capacities, C.
7. You can use other units for temperature.
If you use Kelvin (K), then cg will have the same numbers but the units change to JK-1g-1. This because a change of temperature of 1K is the same as the change of temperature of 1oC.
If you use fahrenheit then you will have to use a value for cg that has the units JoF-1g-1
Find Out the Heat of Solution of Kno3
Source: https://www.ausetute.com.au/heatsolution.html